机器学习导论（15）–神经网络（BP训练）

4,177次阅读

共计 3556 个字符，预计需要花费 9 分钟才能阅读完成。

1969年,作为人工神经网络创始人的明斯基(Marrin M insky)和佩珀特(Seymour Papert)合作出版了《感知器》一书,论证了简单的线性感知器功能有限,不能解决如“异或”(XOR )这样的基本问题,而且对多层网络也持悲观态度。这些论点给神经网络研究以沉重的打击,很多科学家纷纷离开这一领域,神经网络的研究走向长达10年的低潮时期。[1]

1974年哈佛大学的Paul Werbos发明BP算法时，正值神经外网络低潮期，并未受到应有的重视。[2]

1983年，加州理工学院的物理学家John Hopfield利用神经网络，在旅行商这个NP完全问题的求解上获得当时最好成绩，引起了轰动[2]。然而,Hopfield的研究成果仍未能指出明斯基等人论点的错误所在,要推动神经网络研究的全面开展必须直接解除对感知器——多层网络算法的疑虑。[1]

真正打破明斯基冰封魔咒的是，David Rumelhart等学者出版的《平行分布处理:认知的微观结构探索》一书。书中完整地提出了BP算法,系统地解决了多层网络中隐单元连接权的学习问题,并在数学上给出了完整的推导。这是神经网络发展史上的里程碑，BP算法迅速走红，掀起了神经网络的第二次高潮。[1,2]

因此，BP算法的历史意义：明确地否定了明斯基等人的错误观点，对神经网络第二次高潮具有决定性意义。

BP神经网络

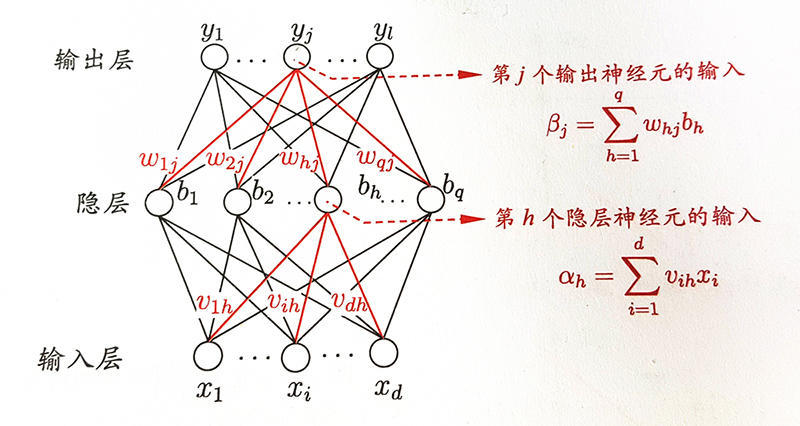
BP神经网络是这样一种神经网络模型，它是由一个输入层、一个输出层和一个或多个隐层构成，它的激活函数采用sigmoid函数，采用BP算法训练的多层前馈神经网络。

BP算法基本思想

BP算法全称叫作误差反向传播(error Back Propagation，或者也叫作误差逆传播)算法。其算法基本思想为：在2.1所述的前馈网络中，输入信号经输入层输入，通过隐层计算由输出层输出，输出值与标记值比较，若有误差，将误差反向由输出层向输入层传播，在这个过程中，利用梯度下降算法对神经元权值进行调整。

BP算法数学工具

BP算法中核心的数学工具就是微积分的链式求导法则。

BP算法的推导

[2]

局部极小值问题

BP算法的缺点，首当其冲就是局部极小值问题。

算法训练非常慢

BP算法本质上是梯度下降，而它所要优化的目标函数又非常复杂，这使得BP算法效率低下。

相应的代码实现如下：

# coding: utf-8

import numpy as np
import math
import random

np.random.seed(0)
# random.seed(0)

# calculate a random number where:  a <= rand < b
def rand(a, b):
    return (b-a)*random.random() + a



def sigmoid(x):
    # f(z) = (e ^ z - e ^ (-z)) / (e ^ z + e ^ (-z))
    # http://ufldl.stanford.edu/wiki/index.php/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
    return math.tanh(x)


def dsigmoid(y):
    # 导数为：f'(z) = 1 - f(z) ^ 2
    return 1.0 - y ** 2


class NN(object):
    def __init__(self, ni, nh, no):
        # 结点数
        self.ni = ni + 1
        self.nh = nh
        self.no = no

        # 值
        self.ai = np.ones((self.ni,))
        self.ah = np.ones((self.nh,))
        self.ao = np.ones((self.no,))


        # 权重
        self.wi = np.random.uniform(-0.2, 0.2, self.ni * self.nh).reshape(self.ni, self.nh)
        self.wo = np.random.uniform(2., -2., self.nh * self.no).reshape(self.nh, self.no)
    

        # 旧的weight
        self.ci = np.zeros((self.ni, self.nh))
        self.co = np.zeros((self.nh, self.no))


    def update(self, inputs):
        assert(len(inputs) == self.ni - 1)
        for i in range(self.ni - 1):
            self.ai[i] = inputs[i]

        for i in range(self.nh):
            s = 0.
            for j in range(self.ni):
                s += self.ai[j] * self.wi[j][i]
            self.ah[i] = sigmoid(s)

        for i in range(self.no):
            s = 0.
            for j in range(self.nh):
                s += self.ah[j] * self.wo[j][i]
            self.ao[i] = sigmoid(s)

    def back_propagate(self, targets, N, M):
        assert(len(targets) == self.no)

        # y = sigmoid(a2 + b), J = 0.5 * (y - t) ** 2, delta_J = (y - t) * y ' * h
        # output_delta = (y - t) * y'
        output_deltas = np.zeros(self.no)
        # output_deltas = [0.] * self.no
        # print(output_deltas)
        
        #使用梯度下降法计算输出层的权重更新计算公式
        for i in range(self.no):
            err = targets[i] - self.ao[i]
            output_deltas[i] = dsigmoid(self.ao[i]) * err

        # hidden_delta = (y - t) * y' * Wo * h'
        # delta_J = (y - t) * y' * Wo * h' * ai
        hidden_deltas = np.zeros(self.nh)
        # hidden_deltas = [0.] * self.nh
        # print(hidden_deltas)
        
        #使用梯度下降法计算隐含层的权重更新计算公式
        for i in range(self.nh):
            err = 0.
            for j in range(self.no):
                err += output_deltas[j] * self.wo[i][j]
            hidden_deltas[i] = dsigmoid(self.ah[i]) * err

        # 这里取两次的delta来逐步改变
        # delta_j = (y - t) * y' * ah
        # W_new = W_old + r1 * delta_J + r2 * delta_J_old
        #更新输出层的权重
        for i in range(self.nh):
            for j in range(self.no):
                change = output_deltas[j] * self.ah[i]
                self.wo[i][j] += N * change + M * self.co[i][j]
                self.co[i][j] = change

        # 更新输入层权重
        for i in range(self.ni):
            for j in range(self.nh):
                change = hidden_deltas[j] * self.ai[i]
                self.wi[i][j] += N * change + M * self.ci[i][j]
                self.ci[i][j] = change

        # 计算错误率
        err = 0.
        for i in range(len(targets)):
            err += 0.5 * (targets[i] - self.ao[i]) ** 2
        return err

    def train(self, patterns, iterations=1000, N=0.5, M=0.1):
        for i in range(iterations):
            err = 0.
            for p in patterns:
                inputs = p[0]
                targets = p[1]
                self.update(inputs)
                #计算累加错误率
                err += self.back_propagate(targets, N, M)
            if i % 100 == 0:
                # self.weights()
                print('error %-.5f' % err)

    def weights(self):
        print("\nInput weights:")
        for i in range(self.ni):
            print(self.wi[i])
        print("\nOutput weights:")
        for i in range(self.nh):
            print(self.wo[i])



def main():
    pat = np.array([
        [[0,0], [0]],
        [[0,1], [1]],
        [[1,0], [1]],
        [[1,1], [0]]
    ])
    nn = NN(2, 2, 1)
    # nn.weights()
    nn.train(pat)

if __name__ == "__main__":
    main()

正文完

请博主喝杯咖啡吧！