共计 1130 个字符,预计需要花费 3 分钟才能阅读完成。
今天继续ESCM的研究,考虑到latex打公式挺麻烦的(我偷懒),我直接粘贴论文里的图,但是我会用白话文来说明,尽量把这个事情说明白。
Lets go!
论文里先是直接给出一个结论,就是pcvr预估偏高的结论

上面的 O R C 代表不同的变量,分别是点击,点击后转化,点击并且转化。
后面那两个不是好理解,可以这么看就是P(转化|点击=1)和P(转化=1,点击=1) ,所以到这里就是条件概率和联合之间的对比。
D表示的是曝光空间,这个也是跟线上真实业务情况对齐的。
这个偏差也是定义在曝光空间上的偏差,论证esmm论文的输出的pcvr是大于 ground truth的,这也是你看到的上面的公式 8 ,它是用期望的方式来说明的。
接下来又直接给出了一个结论
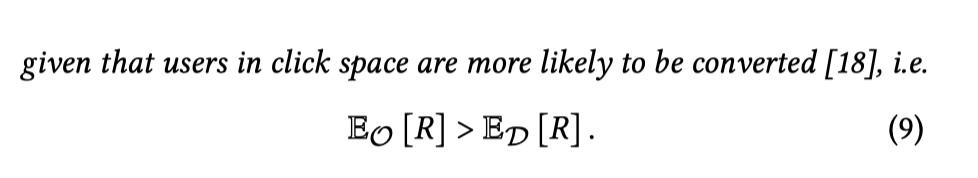
这个结论是要说明在点击空间的转化率比曝光空间的转化率高,这个理解起来好像也没啥问题,一般情况下用户点击一个东西后转化的概率会高一点,我都不喜欢我干嘛还要点它呢,你说是不是?
接下来就开始论证了,首先给出下面的公式,这个公式想要表达的意思是,一个完美的esmm模型能做到点击率和转化率预估值和真实值之间的误差为0。呵呵哒,这个怎么可能嘛,纯粹是从理论的角度来看问题,当然这个不妨碍我们去论证今天想要说的这个问题。
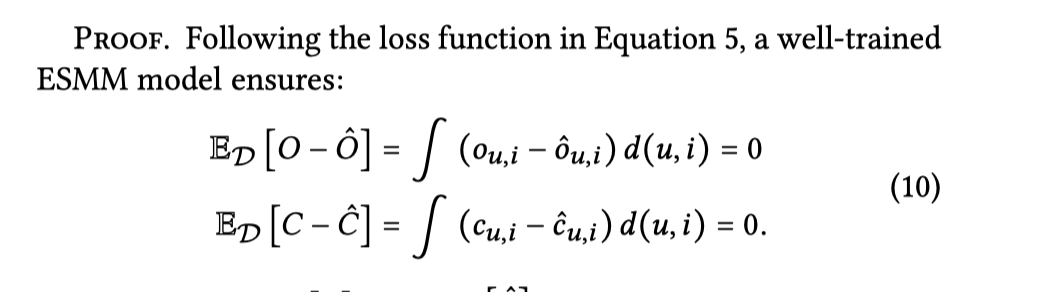
接下来他会把之前的公式 8拿出来推理论证了
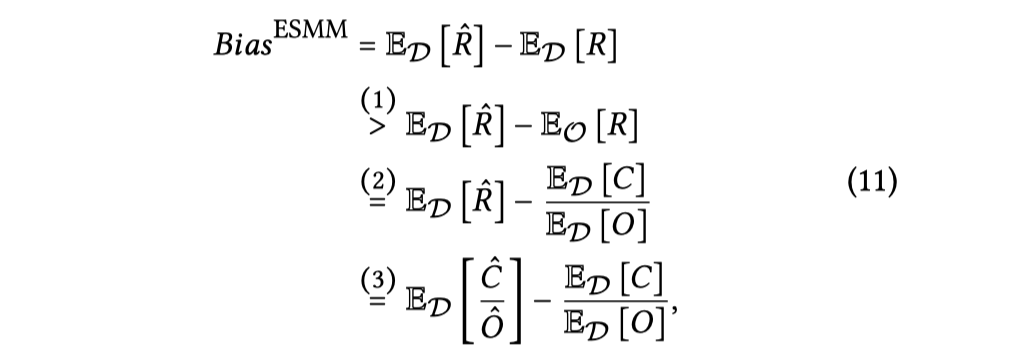
这个公式的
- 第一步:就是沿用公式 9 点结论得到的,点击空间的转化大于曝光空间的转化,所以才有了大于这个结论。
- 第二步:点击空间的转化可以替换为曝光空间的转化除以曝光空间的点击,这不就是纯纯的转换率计算公式嘛,这里就是涉及到空间的转换。
- 第三步:类似第二步同样的道理,说明的都是一样的问题,不过是预估转化率的表述,第二步是真实转换率的描述
一鼓作气继续开干!!!!
这个P 是该联合概率分布,针对点击和转化的联合分布,都是建立在曝光空间上的。

- 第一步:这个就是常规的期望和积分公式之间的表达切换而已,应该不会有太难的理解吧!不然去百度看一下期望的表达?
- 第二步:这里是有esmm本身假设的前提在里面,esmm假设这个点击和转化是相互独立的,所以联合分布被拆开了,这个涉及到概率论了。
- 第三步:这个还是数学公式的转化,联合分布转到各自积分计算
- 第四步:这个又再一次把积分转化为期望的表达
- 第五步:根据杰森不等式得到的结论,这个也是数学公式E(f(x))>=f(E(x))
- 第六步:理想的情况下,预估值和真实值完全相等
到这里基本上就论证出来了,Bias ESMM>0这个事实了。
这也貌似对上了我之前做ESMM遇到的问题,这次算是有一个完备的理论论证,看起来像是那么回事,也算是一种全新的思路去说明这个问题,这也是我看完这篇文章之后比较开心的地方。
灵魂的渴望是对命运的先知!ESMM 你还好?


