cpt序列预测

3,920次阅读

共计 3511 个字符，预计需要花费 9 分钟才能阅读完成。

序列预测是当前深度学习最火热的应用之一。从搭建推荐系统到语音识别再到自然语言处理，序列预测有着广泛的应用前景。

实现序列预测有很多不同的方法，比如利用机器学习中的马尔科夫模型/有向图，深度学习领域中的RNN/LSTM等等。在本文我们会用一种叫做紧凑预测树（Compact Prediction Tree，即CPT）的算法。虽然知道这种算法的人并不多，但它的性能却比很多非常知名的方法还要强大，比如前面提到的马尔科夫模型和有向图。下面就分享一下如何用CPT解决序列预测问题。

序列预测

每当我们想预测一个事件之后可能会发生另一个特定事件时，就需要用到序列预测。序列预测可以广泛应用于多个领域，例如：

网页预取：根据用户访问过的网页序列，浏览器可以预测出用户接下来最可能访问的网页，从而提前加载网页，提升打开网页的速度，优化用户体验。
产品推荐：根据用户在购物车里添加的产品序列，预测用户接下来可能感兴趣的商品，从而为用户推荐产品。
天气预报：根据之前的天气状况预测下一时段的天气。当前解决序列预测的方法

目前解决序列预测最常用的方法是LSTM和RNN，它们已经成为序列建模的热门选择，用于文本、音频等等。不过，它们却有两个基本的问题：

训练时间很长，往往要几十个小时
如果序列中包含了之前训练迭代中未见过的项时，就需要重新训练它们。这个过程代价很高昂，在频繁出现新项目的问题中，就无法使用它们。

认识紧凑预测树（CPT）

紧凑预测树（CPT）这种算法在处理序列预测问题时，往往比传统机器学习方法比如马尔科夫模型和深度学习方法比如自动编码器更加准确。

CPT的一大卖点就是其快速的训练和预测时间。此前CPT算法只在Java代码中实现了，幸好后来出现了Python版。

虽然目前这个库不是很完善，但性能仍然很出色。下面就讲讲CPT算法的内部原理，以及为何它要优于马尔科夫链、直向图这样的机器学习算法。

理解CPT中的数据结构

首先我们有必要了解Python库CPT接受的数据格式。CPT接受两个.csv文件——测试文件和训练文件。训练文件包含训练序列，测试文件同样包含序列，且需要预测每个序列的接下来的3项。为了清楚起见，在测试文件和训练文件中的序列定义如下：

  1,2,3,4,5,6,7
  5,6,3,6,3,4,5
  .
  .
  .
复制代码

注意，序列的长度可以不相同。此外，独热编码序列不适用。 CPT算法用到了3种基本的数据结构，我们下面简单解读。

1 预测树

预测树是一种由节点组成的树，每个节点有3个元素：

数据项（item）：存储在节点中的实际数据项
子节点（children）：该节点的所有子节点的列表
父节点（parent）：指向此节点的父节点的链接或引用

预测树基本上是一种trie数据结构，将整个训练数据压缩为一颗树的形式。如果你不清楚trie数据结构的工作方式，可以参看下面两个序列的trie结构图：

序列1: A, B, C
序列2: A, B, D

Trie数据结构首先以序列A，B，C的第一个元素A开始，将A添加到根节点上。然后将B添加到A，再将C添加到B。对于每个新的序列，trie会再次从根节点开始，若某个元素已经被添加至数据结构中，则跳过。

最终数据结构如上所示。这就是预测树高效压缩训练数据的方法。

2 倒排索引

倒排索引是一种字典，其中的键是训练集中的项，值为出现该项的序列的集合。例如：序列1: A,B,C,D 序列2: B,C 序列3: A,B 上述序列的倒排索引如下所示：

II = {
‘A’:{‘Seq1’,’Seq3’},
’B’:{‘Seq1’,’Seq2’,’Seq3’},
’C’:{‘Seq1’,’Seq2’},
’D’:{‘Seq1’}
}

3 查找表

查找表也是一种字典，其中的键是序列的ID，值为预测树中的序列的终端节点。例如：

序列1: A, B, C
序列2: A, B, D

LT = {
“Seq1” : node(C),
“Seq2” : node(D)
}

理解CPT中训练和预测的工作原理

我们会通过一个例子巩固对CPT算法的训练和预测过程的理解。下面是例子的训练集：

可以看到，上述训练集有3个序列。我们用ID表示它们：seq1，seq2和seq3。A,B,C和D都是训练数据集中的不同的唯一项。

训练阶段

训练阶段会同时搭建预测树、倒排索引、查找表。我们现在看看整个训练过程阶段：

第一步：插入A，B，C

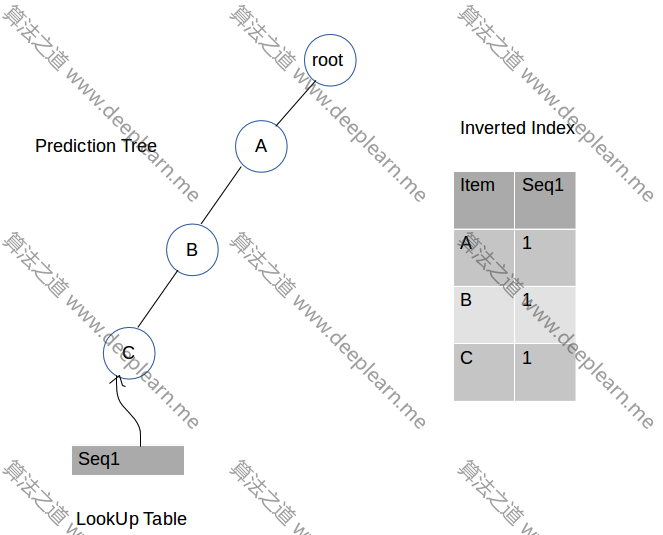
我们得到一个根节点，以及一个初始设置为根节点的当前节点变量。

我们先从A开始，查看A是否为根节点的子节点。如果不是，我们就将A添加到根节点的子节点列表中，在带有值为seq1的倒排索引中添加一个A的条目，然后将当前节点移动到A。

我们接着看下一个项，也就是B，查看B是否作为当前节点（也就是A）的子节点存在。如果不是，就把B添加到A的子列表中，在带有值为seq1的倒排索引中添加一个B的条目，然后将当前节点移动到B。

我们然后重复上面的过程，直至完成添加seq1的最后一个元素。最后，我们会将seq1的最后一个节点，也就是C，添加到键等于“seq1”和值等于节点C的查找表中。

第二步：插入A和B

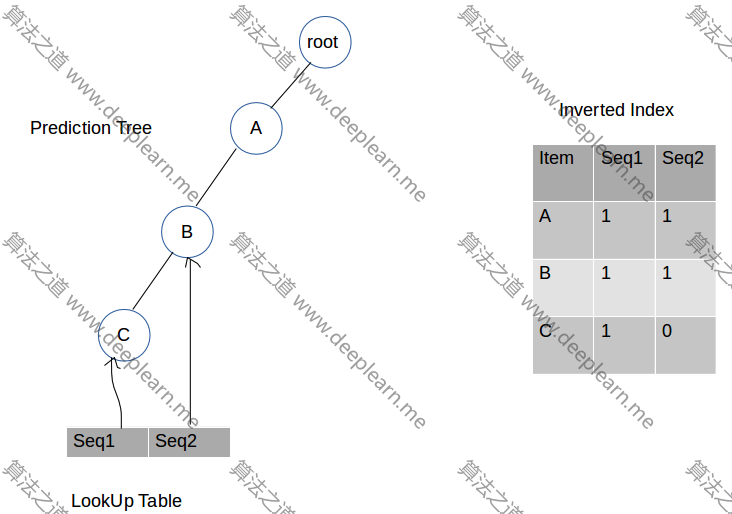
第三步：插入A，B和C

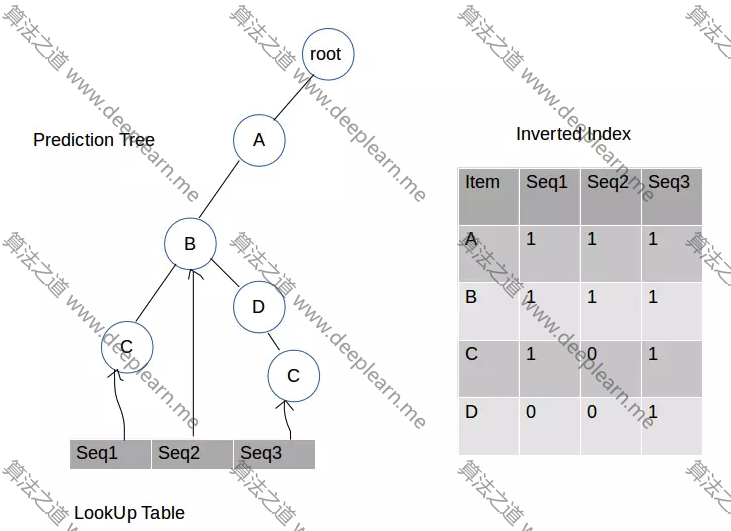
第四步：插入B和C

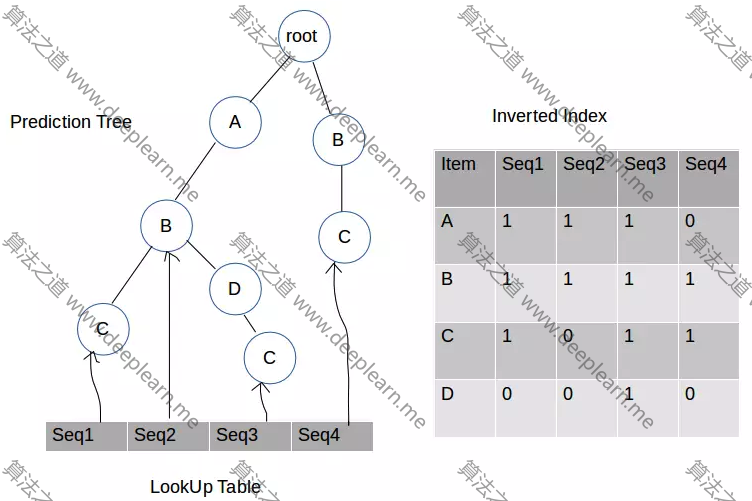
我们一直持续这个过程直到用尽训练数据集中的每一行（记住，每一行代表一个序列）。我们现在已经准备好了所有需要的数据结构，开始在测试数据集中做预测。下面我们看看预测过程。

预测阶段

预测阶段中会以迭代的方式，为测试集中数据的每个序列做出预测。对于单个行，我们用倒排索引找到和该行相似的序列。然后我们找到相似序列的后续序列，将后续序列中的项添加到计数字典中，并给出分值。最后，用计数字典返回分数最高的项，将它作为最终预测值。我们会看到每一步的详细情况，更深入的了解CPT。

目标序列——A,B

第一步：找到和目标序列相似的序列。

通过用倒排索引找到和目标序列相似的序列，通过以下几步查找：

找到目标序列的唯一项，
查找存在特定唯一项的序列ID集合，
然后取所有唯一项集合的交集。

例如：

存在A项的序列集= {‘Seq1’,’Seq2’,’Seq3’}
存在B项的序列集= {‘Seq1’,’Seq2’,’Seq3’,’Seq4’}
和目标序列相似的序列=集合A和集合B的交集= {‘Seq1’,’Seq2’,’Seq3’}

第二步：找到和目标序列相似的每个序列的后续序列

对于每个相似序列，后续序列定义为在相似序列中目标序列最后一项发生后，减去目标序列中存在的项之后的最长子序列。

我们通过下面的例子更好的理解：

目标序列=[‘A’,’B’,’C’] 相似序列= [‘X’,’A’,’Y’,’B’,’C’,’E’,’A’,’F’]

目标序列的最后一项=‘C’
相似序列中‘C’最后发生后的最长子序列= [‘E’,’A’,’F’]

后续序列=[‘E’,’F’]

第三步：把后续序列中的元素及其分值添加至计数字典中

将每个相似序列的后续序列的元素与得分添加到字典中。例如，继续上面的例子。后续序列[‘E’,’F’]中所有项的分值计算如下：

计数字典的初始状态= {},是一个空字典
如果字典中不存在该项，那么，
分值=1 + （1/相似序列的数量）+（1/计数字典中当前项的数量+1）*0.001

否则，
分值=（1+（1/相似序列的数量）+（1/计算表中当前项的数量）*0.001） * 原来的分值
那么对于元素E，也就是后续序列的第一个项，分值会是：
分值[E]=1 + (1/1) + 1/(0+1)*0.001 = 2.001
分值[F]=1 + (1/1) + 1/(1+1)*0.001 = 2.0005

经过如上计算后，计数字典会如下所示： counttable = {‘E’ : 2.001, ‘F’: 2.0005}

第四步：用计算字典做出预测

最终，将计数字典中返回的值最大的键作为预测值。在我们上面所举的例子中，E作为预测值返回。

创建模型，做出预测

第一步：从这里克隆GitHub库：

github.com/analyticsvi…

git clone github.com/NeerajSarwa…

第二步：用如下代码读取.csv文件训练你的模型，做出预测。

#导入CPT文件中的全部内容
from CPT import *

#创建CPT类的一个对象
model = CPT()

#读取训练和测试文件，将其转换为数据和目标
data, target = model.load_files(“./data/train.csv”,”./data/test.csv”)

#训练模型
model.train(data)

#用测试数据集做出预测
predictions = model.predict(data,target,5,1)