LTR排序之pair-wise-ranknet算法TensorFlow实现

共计 5589 个字符，预计需要花费 14 分钟才能阅读完成。

在之前的有一篇文章给出了pointwise之prank算法说明以及实现，这一篇文章会讲解pairwise。

写这篇文章之前也看了很多篇博客包括原版论文，在这里自己尽量用白话 的方式让读者理解这个看似很厉害的方法。

乍一看pair，英文直接翻译就是一对的意思，哈哈，这个排序方法与组队有很大的关系，究竟组队会在哪里体现呢？等会就知道了

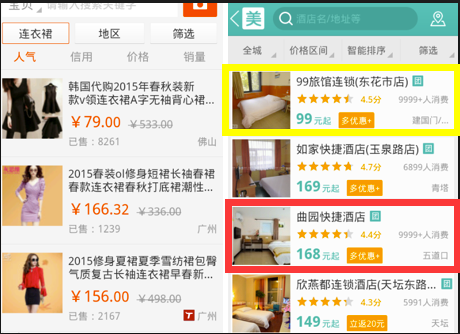
先看两幅图，为什么要出现组队情况

在上图中红色的框是用户点击的框，黄色的框虽然排在前面但是用户没有点击，因此按照我们正常的理解红色的商品应该放在前面更符合用户的习惯，但是现在的

结果是商品排在黄色的商品后面，所以这个排序还是存在一定改善的空间。此时出现了两个商品的对比，也就是说红色的商品相对黄色的商品较好，此处也仅仅是相对而言，

把这两个商品单独拎出来看的话，那肯定是红色框框里面的商品更好。

这篇文章提到的主题就是pariwise，这时候pair的意思就体现出来了。这个方法的核心就是先将商品组合起来，组合还是有先后之分的，我们定义一下几个规则

给出两个商品\( i,j \)，如果i比j更好（更符合用户的口味）那么定义 \( <i,j>,1\) 如果二者的相关性相同也就是都是50%概率, \( <i,j>,0\) 除此之外就是\( <i,j>,-1\)

机器学习排序还是需要找到一个函数\( F(x)\) 来给我们的样本打分排序,如果我们的样本i比样本j更好，那么的对应的分数\( F(i)>F(j)\)

假设上面的打分函数是个线性模型，那么函数中有很多的参数需要我们去求解，这些参数该如何求解？
这个跟逻辑回归就有点像了，在逻辑回归中我们给定了样本，然后我们想要在样本集上最大化p(y|x)，这个可以通过最大似然估计的方法来求解。

首先我们要给出概率定义公式：

样本 \(x_i\) 的排名得分用 \(o_i\) 表示，定义 \(o_{i,j}=o_i−o_j\) ，如果 \(o_{i,j}>0\) 就说明 xi 名次高于 xj 。将这个排名概率化，定义：

\[P_{i,j}=\frac{e^{o_{i,j}}}{1+e^{o_{i,j}}} \]

表示 xi 排名高于 xj 的概率。可以发现， \(o_{i,j}=0\) 的时候有 \(P_{i,j}=0.5\) 。

接下来就有一个有意思的结论：对于任何一个长度为n的排列，只需要知道n-1个相邻item的概率 Pi,i+1 ，就可以推断出来任何两个item的排序概率。

例如已知 Pi,k 和 Pk,j ，那么 Pi,j 可以使用下面公式推断出来：
\[ \begin{matrix} P_{i,j}&=&\frac{e^{o_{i,j}}}{1+e^{o_{i,j}}}\\ &=&\frac{e^{o_i-o_j}}{1+e^{o_i-o_j}} \\ &=& \frac{e^{o_i- o_k + o_k + o_j}}{1+e^{o_i-o_k + o_k -o_j}}\\&=& \frac{e^{o_{i,k} + o_{k,j}}}{1+e^{o_{i,k} + o_{k,j}}} \\&=& \frac{P_{i,k}\ P_{k,j}}{1+2P_{i,k}\ P_{k,j}\ -P_{i,k}\ -P_{k,j}}\end{matrix} \]

其中最后一步的推倒使用了 Pi,j 和 oi,j 的定义的推导，即：
\[ o_{i,j} = \ln \frac{P_{i,j}}{1-P{i,j}}\]

所以，我们如果想要知道任何两个item的排列关系，不需计算 \( C_n^2\) 种组合，n-1个 Pi,i+1 已经含有了所有组合的排序信息，这个就是RankNet将 \( O(C_n^2)\) 复杂度的问题，变为 O(n) 问题的理论基础。

下面给出损失函数的定义
\[ \begin{matrix}C(o_{ij})&=&-\hat{P}_{i,j} \ln P_{ij} – (1-\hat{P}_{ij})\ln (1-P_{ij})\\&=&-\hat{P}_{ij} o_{ij}+\ln (1+e^{o_{ij}})\end{matrix} \]
跟逻辑回归的一模一样，感叹一下

上述公式有两个概率，其中一个在之前的描述中已经给出来了，还有一个\( \hat{P}_{i,j} \)计算方法未给出，这个概率是真实的i和j的相对顺序的概率，下面给出计算公式：
\[ \hat{P}_{i,j}=\frac{1}{2}(1+S_{ij}) \]
上述公式中\(S_{ij}\)就是在前面描述的情况：给出两个商品\( i,j \)，如果i比j更好（更符合用户的口味）那么定义 \( <i,j>,S_{ij}=1\) 如果二者的相关性相同也就是都是50%概率, \( <i,j>,S_{ij}=0\) 除此之外就是\( <i,j>,S_{ij}=-1\)

呀呀呀，上面描述的都是ranknet算法，pairwise的算法还有其他的，有兴趣可以继续了解，博主也会去学习

TensorFlow的代码保存在mac上面，明天抽个时间贴到这里来。。。。，先去洗澡睡觉觉了

# -*- coding: utf-8 -*-
# @Time    : 2018/3/27 上午10:55
# @Author  : Tomcj
# @File    : tensor_ranknet.py
# @Software: PyCharm
import  tensorflow as tf
import numpy as np

BATCH_SIZE=100
y_train=[]
X_train=[]
Query=[]
array_train_x1=[]
array_train_x0=[]

feature_num = 46
h1_num = 10
def extractFeatures(split):
    '''
    获取特征
    '''
    features = []
    for i in range(2, 48):
        features.append(float(split[i].split(':')[1]))
    return features


def extractQueryData(split):
    '''
    获取以下数据quryid documentid等
    Format:
    
    '''
    queryFeatures = [split[1].split(':')[1]]
    queryFeatures.append(split[50])
    queryFeatures.append(split[53])
    queryFeatures.append(split[56])

    return queryFeatures
def get_microsoft_data():
    '''
    获取基础样本特征数据
    :return:
    '''
    with open('/Users/leiyang/RankNet/Data/train.txt','r') as fp:
        for data in fp:
            split = data.split()
            y_train.append(int(split[0]))
            X_train.append(extractFeatures(split))
            Query.append(extractQueryData(split))

def get_pair_feature(y_train,Query):
    '''
    获取组合样本特征
    :return:
    '''
    pairs = []
    tmp_x0=[]
    tmp_x1=[]
    for i in range(0, len(Query)):
        for j in range(i + 1, len(Query)):
            # Only look at queries with the same id
            if (Query[i][0] != Query[j][0]):
                break
            # Document pairs found with different rating
            if (Query[i][0] == Query[j][0] and y_train[i] != y_train[j]):
                # Sort by saving the largest index in position 0
                if (y_train[i] > y_train[j]):
                    pairs.append([i, j])
                    tmp_x0.append(X_train[i])
                    tmp_x1.append(X_train[j])
                else:
                    pairs.append([j, i])
                    tmp_x0.append(X_train[j])
                    tmp_x1.append(X_train[i])

    array_train_x0 = np.array(tmp_x0)
    array_train_x1=np.array(tmp_x1)
    print('Found %d document pairs' % (len(pairs)))
    return pairs,len(pairs),array_train_x0,array_train_x1


with tf.name_scope("input"):
    x1 = tf.placeholder(tf.float32,[None, feature_num],name="x1")
    x2 = tf.placeholder(tf.float32,[None, feature_num],name="x2")

#添加隐层节点
with tf.name_scope("layer1"):
    with tf.name_scope("w1"):
        w1 = tf.Variable(tf.random_normal([feature_num, h1_num]), name="w1")
    with  tf.name_scope("b1"):
        b1 = tf.Variable(tf.random_normal([h1_num]), name="b1")

    #此处没有添加激活函数
    with tf.name_scope("h1_o1"):
        h1_o1 = tf.matmul(x1,w1) + b1
        h1_o1=tf.nn.relu(h1_o1)


    with tf.name_scope("h2_o1"):
        h1_o2 = tf.matmul(x2, w1) + b1
        h1_o2 = tf.nn.relu(h1_o2)

#添加输出节点
with tf.name_scope("output"):
    with tf.name_scope("w2"):
        w2 = tf.Variable(tf.random_normal([h1_num, 1]), name="w2")

    with tf.name_scope("b2"):
        b2 = tf.Variable(tf.random_normal([1]))

    h2_o1 = tf.matmul(h1_o1, w2) + b2
    h2_o2 = tf.matmul(h1_o2, w2) + b2
    h2_o1=tf.sigmoid(h2_o1)
    h2_o2=tf.sigmoid(h2_o2)

#根据输出节点计算概率值
with tf.name_scope("loss"):
    # o12 = o1 - o2
    h_o12 = h2_o1 - h2_o2
    pred = 1/(1 + tf.exp(-h_o12))
    #此处的label_P就是真实的概率，因为前面组pair数据已经人为将相关的样本放在
    #前面，所以Sij均为1，所以计算的结果就是1
    lable_p = 1

    cross_entropy = -lable_p * tf.log(pred) -(1-lable_p) * tf.log(1-pred)

    reduce_sum = tf.reduce_sum(cross_entropy)
    loss = tf.reduce_mean(reduce_sum)

with tf.name_scope("train_op"):
    train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)


with tf.Session() as sess :
    # step 1 解析microsoft数据集
    get_microsoft_data()
    #step 2 获取 pair组合
    pairs,datasize,array_train_x0,array_train_x1=get_pair_feature(y_train,Query)
    init = tf.global_variables_initializer()
    sess.run(init)
    for epoch in range(0,10000):
        start=(epoch*BATCH_SIZE)%datasize
        end=min(start+BATCH_SIZE,datasize)
        sess.run(train_op, feed_dict={x1: array_train_x0[start:end,:], x2: array_train_x1[start:end,:]})
        if epoch % 1000== 0 :
            l_v = sess.run(loss, feed_dict={x1:array_train_x0, x2:array_train_x1})

            result_0=sess.run(h2_o1,feed_dict={x1:array_train_x0, x2:array_train_x1})
            result_1=sess.run(h2_o2,feed_dict={x1:array_train_x0, x2:array_train_x1})
            #使用所有的样本计算模型预测的准确率
            print  np.sum(result_0>result_1)*1.0/datasize
            # print  sess.run(cross_entropy,feed_dict={x1:array_train_x0, x2:array_train_x1})
            # print "------ epoch[%d] loss_v[%f] ------ "%(epoch, l_v)

相关数据下载
[fanctdl filename=’microsoft数据集’ filesize=’2G’ href=’http://research.microsoft.com/en-us/projects/mslr/’ filedown=’微软官方下载’][/fanctdl]