共计 1460 个字符,预计需要花费 4 分钟才能阅读完成。
使用L1和L2正则化的使用,在许多代价函数中经常出现,也许你知道了L1会产生稀疏解,L2会防止过拟合之类的结果,这篇文章博主带你其中的秘密
l1 和l2简单介绍这篇文章有简单的介绍,这篇文章也会在讲一讲
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。下图是Python中Lasso回归的损失函数,式中加号后面一项α||w||1即为L1正则化项。
先给出基于线性回归的代价函数例子:
其中L1的优化目标代价函数如下:
\[ \min \limits_{w} \frac{1}{2n} \vert\vert Xw-y\vert\vert^2_2+\alpha\vert\vert w \vert\vert_1 \]
其中L2的优化目标代价函数如下:
\[ \min \limits_{w} \frac{1}{2n} \vert\vert Xw-y\vert\vert^2_2+\alpha\vert\vert w \vert\vert^2_2 \]
在简单说一下1范数和2范数的定义,1范数就是绝对值之和,2范数是先平方求和在取绝对值
稀疏模型与特征选择
上面提到L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。为什么要生成一个稀疏矩阵?
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
究竟L1是如何产生稀疏模型的?
我们先把之前的公式给简化一下
优化的目标函数改为
\[ J=J_0+L\]
上面的平方损失函数就用J0代替,正则化项就用L代替
我们优化的目标就是要求出一个w使得当前的J取值最小,按照正常的思维肯定想通过求导的方式来求解最优w值,但是L中包含了绝对值,因此是不可导的,所以直接求解也求解不到
为了直观的了解,我们可以将J0和L绘制图像来说明,我们所要求解的w需要保证J0和L同时最小以达到代价函数最小化的目的。下面我们以w为二维变量来分析
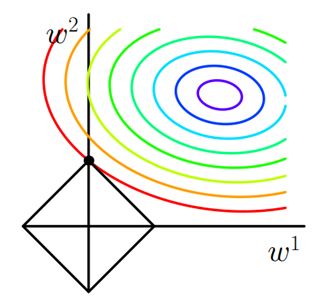
J0本质上就一个圆,其中变量w是动态参数,如果我们调节w就会得到一系列的圆,这也是你在上图中看到这么多圆线的原因,上图中其实假设了w参数只有二维,这样方便在图中表示,与此同时L的图像是一个旋转90度的矩形,图像中二者交点的位置就是可能出现最优解的地方,你会发现二者相交出现极大可能的位置就是顶点处,矩形顶点的地方肯定是由其中一个w为0的,w为0则表示其中一个特征并不是我们需要的特征可以忽略不计,这就说明了L1会产生稀疏解的原因
到这里应该可以理解L1的真面目了,说道这里其实有些人应该可以知道L2为什么不会产生稀疏解了的原因,下面我们也是类似上面的解释方式来说明L2问题,
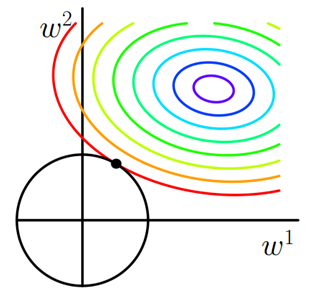
L1和L2区别主要在于L不一样,对于L2而言L在图像中就是一个圆了,如下所示
从上图就会发现二者相交不会轻易的发生在定点处了,因此w的值很难会出现为0的现象,当然会有w值很小的情况,也可以说明当前的特征重要性比较低